중위표현식을 후위표현식으로 바꿔서 연산하기(feat. 문자열 사칙연산, 이진트리)
문자열로 들어온 사칙연산을 어떻게 풀까?
알고리즘 문제를 풀다보면 "1 + (2 - (3 * 7)) + (5 * 10)" 이런 문자열 형식의 사칙연산을 풀어내는 문제들이 가끔 나온다.
우리는 직관적으로 가장 안쪽 괄호부터 계산하고, 괄호가 없다면 곱셈/나눗셈, 덧셈/뺄셈 순으로 먼저 계산한다는 것을 알고 있다. 하지만 컴퓨터는 항상 그렇지 않다..!
그래서 문자열 형식의 사칙연산을 하나하나 쪼개 우선순위를 부여해주고, 그 우선순위에 따라 차례대로 연산을 해나가도록 알고리즘을 짜야 한다.
이를 풀어내기 위해 중위표현식을 후위표현식으로, 후위표현식을 이진트리로 만들어 트리를 탐색하면서 값을 연산할 것이다.
표현식(Expression)
위키피디아에 따르면, 표현식은 값을 알 수 있는 어떠한 형태의 구문이다. 수학에서 수식을 컴퓨터공학에선 표현식이라고 부르는 것 같다.
알고리즘으로 만들 사칙연산 뿐만 아니라, 변수에 값을 할당하는 것도 표현식이 될 수 있다고 한다.
지금은 사칙연산을 컴퓨터가 이해할 수 있는 표현식으로 변환하는 것이 목적이기 때문에 다른건 됐고 연산을 할 수 있는 표현식에 대해서 알아보자!
중위, 후위, 전위 표현식(Infix, Postfix, Prefix Expression)
중위, 후위, 전위 표현식은 표현식을 서술할 수 있는 각기 다른 방법이다. 결과값은 동일하다. (정의 출처)
우리가 알고 있는 기본적인 형태의 표현식은 중위표현식으로, 연산자가 피연산자 중간에 위치한다. 사칙연산을 위한 연산자 뿐만 아니라 중위표현식에선 괄호가 값에 영향을 미친다.
후위표현식은 연산자가 피연산자 뒤에 위치하는 것, 전위표현식은 연산자가 피연산자 앞에 위치하는 것이다.
이진트리(Binary Tree)
부모-자식으로 연결된 트리 구조에서, 부모가 단 두개의 자식만을 갖는 트리를 이진 트리라고 한다.
자료구조중 힙(Heap)을 구현할 때 이진 트리를 사용한다.
이진 트리는 두 개의 자식을 가지므로 보편적으로 왼쪽과 오른쪽으로 나눌 수 있다.
A 1
/ \ / \
B C 2 3
/ \ / \ / \
D E F G 4 5
트리는 위와 같은 방식으로 나타낼 수 있다.
링크드 리스트의 개념을 활용해 각 노드가 왼쪽과 오른쪽 자식 노드를 담고 있어도 되지만, 노드 생성시마다 새 노드를 메모리에 할당해야 하므로 배열을 활용하여 트리를 만드는 것이 더 경제적이어보인다. (C에서 malloc, free를 이용해 동적할당 할 때의 이야기지만 Swift에서 객체 생성하는데도 비용이 들테니 동일하게 적용될 수 있다고 생각한다. 아니라면 댓글 부탁드립니다!)
그럼 저 구조를 배열에서 어떻게 나타낼까?
배열에서는 인덱스를 사용해 부모와 자식 노드를 구분하면 된다.

위 그림처럼 노드의 인덱스가 i일 때, 그 노드의 왼쪽 자식의 인덱스는 (i * 2) + 1, 오른쪽 자식의 인덱스는(i * 2) + 2가 된다.
이걸 활용해 위의 트리를 배열로 나타내면
[A, B, C, D, E, F, G, nil, nil, nil, nil, nil, nil, nil, nil]
[1, 2, 3, nil, nil, 4, 5, nil, nil, nil, nil]
이 된다.
여기서 배열의 개수는 전체 노드의 개수 곱하기 2에 1을 더한 값과 같다. (1 더하는건 인덱스가 0부터 시작하기 때문)
nil은 머임?
리프 노드, 즉 끝 노드를 나타낼 때 NULL, nil 등을 사용했다.
배열에서도 마찬가지로 해당 노드가 마지막 노드라는 것을 나타내기 위해 왼쪽과 오른쪽 노드에 각각 nil(Swift)을 추가해줬다.
왜 후위표현식과 이진트리 개념을 활용해야하지?
프로그래밍을 위해 구현된 자료구조중 수식을 표현하는 이진 트리가 있는데 이를 Binary Expression Tree라고 한다.
이는 위에서 설명한 것처럼 이진 트리로 구성돼있고, 각 표현식을 연산하는 방법으로 일반적으로 후위 순회를 채택한다.
잘 알려져있는 자료구조를 활용해 조금 더 알고리즘을 쉽게 만들기 위해 중위표현식을 후위표현식으로, 후위표현식을 이진 트리로, 이진 트리를 후위 순회하면서 값을 내도록 했다.
구현하기
중위표현식 -> 후위표현식
String으로 들어온 중위표현식을 Array<String> 형식의 후위표현식(배열)으로 값을 반환하는 함수를 만들었다.
여기서 인자로 들어가는 infixExpression은 1+(2+3)*7과 같이 공백 없이 괄호 포함된 문자열의 상태다. 공백이 있거나 괄호가 없는 조건이라면 infixExpression의 각 원소를 순회하기 전 split을 사용하고, 연산자 우선순위에 따라 스택 push/pop하는 과정에서 괄호를 제거하면 된다.
/// 중위표현식을 후위표현식의 배열로 만들기
func infixToPostfix(_ infixExpression: String) -> [String] {
// 연산자 우선순위를 위한 딕셔너리
let operatorPriority: [Character: Int] = ["(": 0, ")": 0, "+": 1, "-": 1, "*": 2, "/": 2]
// 반환할 후위표현식 배열
var postfixExpression: [String] = []
// 우선순위대로 push/pop될 연산자 스택
var operatorStack: [Character] = []
// 중위표현식에서 각 문자(토큰) 판별
for token in infixExpression {
// 우선순위가 있으면 연산자
// 1. 괄호 체크
// 2. 우선순위 체크
if let priority = operatorPriority[token] {
// 괄호일때
if priority == 0 {
// 왼쪽 괄호면 스택에 추가
if token == "(" {
operatorStack.append(token)
}
// 오른쪽 괄호면 스택에서 "(" 나올 때까지 removeLast()하고 후위표현식 배열에 추가
else {
while !operatorStack.isEmpty {
let lastOperator = operatorStack.removeLast()
if lastOperator == "(" {
break
} else {
postfixExpression.append(String(lastOperator))
}
}
}
}
// 괄호 아닌 연산자일때
else {
// 연산자 스택의 마지막 연산자보다 현재 연산자의 우선순위가 낮거나 같으면 먼저 후위표현식 배열에 추가
while !operatorStack.isEmpty && priority <= operatorPriority[operatorStack.last!]! {
let lastOperator = String(operatorStack.removeLast())
postfixExpression.append(lastOperator)
}
// 현재 연산자의 우선순위가 높으면 연산자 스택에 현재 연산자 추가
operatorStack.append(token)
}
}
// 우선순위가 없으면 피연산자
// String으로 변환 후 배열에 추가
else {
postfixExpression.append(String(token))
}
}
// 연산자 스택에 남아 있는 모든 연산자들 후위표현식 배열에 추가
while !operatorStack.isEmpty {
let lastOperator = String(operatorStack.removeLast())
postfixExpression.append(lastOperator)
}
return postfixExpression
}
후위표현식 -> 이진 트리(배열)
Array<String> 형식으로 나온 후위표현식 배열을 배열 형태의 이진 트리로 변환한다.
후위표현식이므로 가장 우선순위가 높은 연산자가 맨 뒤에 있고, 해당 연산자의 피연산자는 각각 맨 뒤에서 -1, -2에 위치한다. 이를 재귀적으로 타고 내려가면서 배열에 추가해주면 된다.
/// 후위연산자 배열을 수식트리로 만들기
/// tree는 postfixExpression 배열의 개수 * 2 + 1, 각 원소는 nil로 초기화한 후 사용해야 함
func buildExpressionTree(
with postfixExpression: inout [String],
_ tree: inout [String?],
_ index: Int
) {
guard let token = postfixExpression.popLast()
else { return }
switch token {
case "+", "-", "*", "/":
// 루트가 됨
// 오른쪽 트리 만들러 내려감
// 왼쪽 트리 만들러 내려감
tree[index] = token
buildExpressionTree(with: &postfixExpression, &tree, index * 2 + 2)
buildExpressionTree(with: &postfixExpression, &tree, index * 2 + 1)
default:
// 리프가 됨
tree[index] = token
}
}
여기서 tree는 함수를 사용하기 전 정의되어야한다.
// 예시
var postfixExpression = infixToPostfix("(1+2)-(7*8)")
var tree: [String?] = Array(repeating: nil, count: postfixExpression.count + 1)
buildExpressionTree(&postfixExpression, &tree, 0)
이진 트리 후위 순회하며 연산
만들어진 이진 트리(수식 트리)를 후위 순회하며 연산해나가면 끝이다.
후위 순회: 왼쪽자식노드 - 오른쪽자식노드 - 부모노드 순서로 순회하는 것.
/// 수식트리를 탐색하면서 결과값 내기
func valueOfExpressionTree(with tree: [String?], _ index: Int) -> Int {
guard index < tree.count,
let node = tree[index]
else { return 0 }
let leftIndex = index * 2 + 1
let rightIndex = index * 2 + 2
// 왼쪽, 오른쪽 숫자 혹은 연산값 나올때까지 재귀
let leftNum = valueOfExpressionTree(with: tree, leftIndex)
let rightNum = valueOfExpressionTree(with: tree, rightIndex)
switch node {
case "+", "-", "*", "/":
if node == "+" { return leftNum + rightNum }
else if node == "-" { return leftNum - rightNum }
else if node == "*" { return leftNum * rightNum }
else { return leftNum / rightNum }
default:
return Int(node)!
}
}
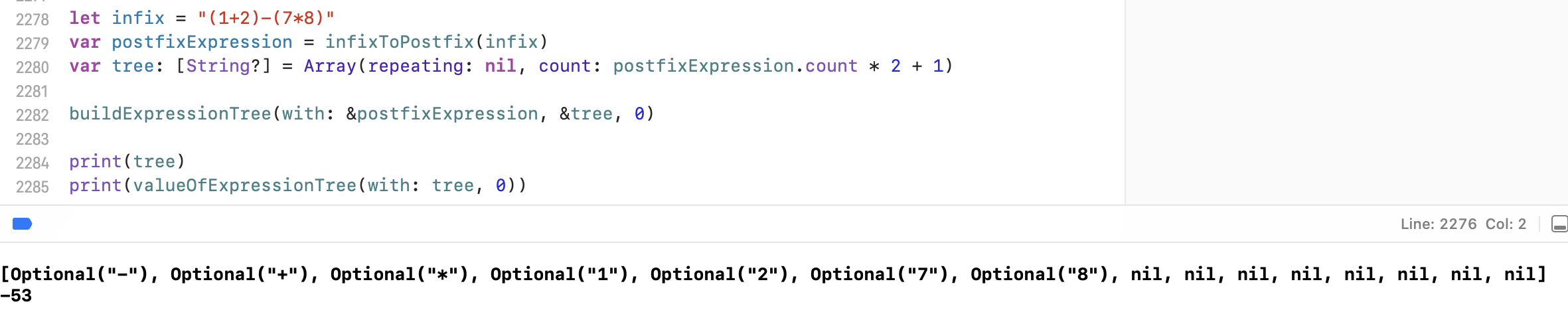
결과
위 코드를 돌려보면 다음과 같이 나온다.


댓글남기기