스위프트 알고리즘 클럽 번역, 너비우선탐색(BFS)

너비 우선 탐색(BFS)

✔︎ 이 글은 Swift Algorighm Club 의 문서를 번역한 글입니다.

너비 우선 탐색(Breadth-First Search)

이 토픽은 여기서 배울 수 있습니다.

너비 우선 탐색은 트리나 그래프를 순회하거나 찾는 알고리즘이다. 소스 노드에서 시작해 다음 레벨의 근방 노드로 움직이기 전까지 가장 가까이에 있는 노드부터 탐색해나간다.

너비 우선 탐색은 방향성이 있는 그래프와 방향성이 없는 그래프 모두에 사용될 수 있다.

움직이는 예시

다음은 너비 우선 탐색이 그래프에서 어떻게 작동하는지를 보여 준다.

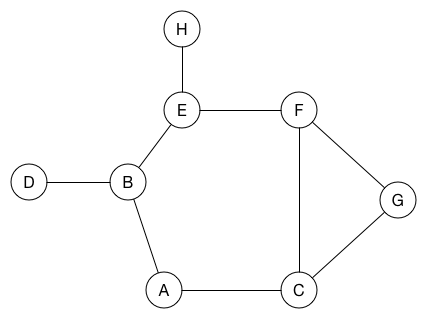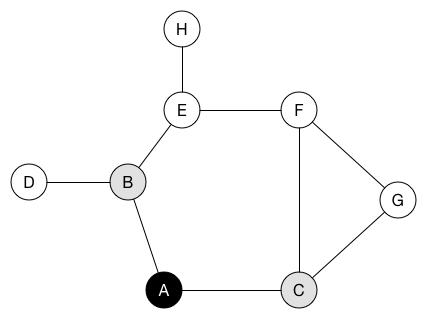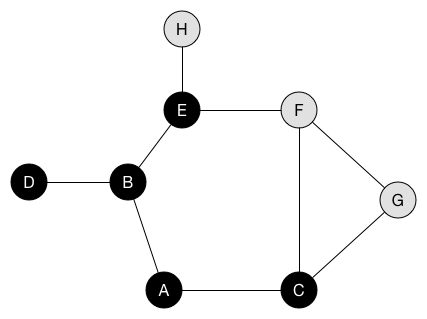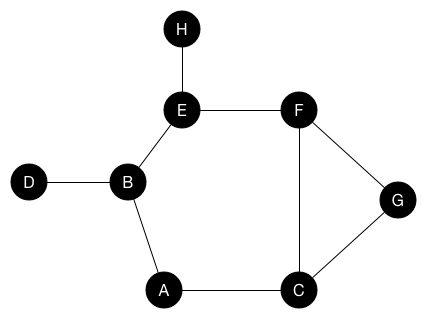
노드를 방문하면 검정으로 칠하자. 그와 동시에 인접한 노드를 큐에 넣는다. 위의 애니메이션에서 인큐(enqueue)됐지만 아직 방문하지 않은 노드를 회색으로 표시했다.

위의 애니메이션 예시를 따라가보자. 소스노드 A 로 시작하고, 이를 큐에 추가한다. 애니메이션에서 A 노드가 회색으로 보이게 되는 것과 같다.

queue.enqueue(A)

큐는 [ A ] 가 된다. 큐의 동작은 다음과 같다. 큐에 노드가 있을 때, 큐의 가장 첫번째 노드를 방문하고, 아직 방문하지 않은 인접한 노드를 곧바로 인큐하는 것이다.

그래프 순회를 시작하기 위해 큐에서 첫번째 노드 A 를 꺼내고 이를 검정색으로 칠한다. 그리고 인접한 노드 B 와 C 를 인큐한다. 이 동작은 두 노드를 회색으로 만든다.

queue.dequeue()   // A
queue.enqueue(B)
queue.enqueue(C)

큐는 이제 [ B, C ] 가 된다. B 를 디큐(dequeue)하고, B 의 인접 노드인 D 와 E 를 인큐한다.

queue.dequeue()   // B
queue.enqueue(D)
queue.enqueue(E)

큐는 [ C, D, E ] 가 된다. C 를 디큐하고, C 의 인접 노드인 F 와 G 를 인큐한다.

queue.dequeue()   // C
queue.enqueue(F)
queue.enqueue(G)

큐는 [ D, E, F, G ] 가 된다. 인접한 노드가 없는 D 를 디큐한다.

queue.dequeue()   // D

큐는 [ E, F, G ] 고, E 를 디큐하고 그것의 유일한 인접 노드인 H 를 인큐한다. E 의 인접 노드에는 B 도 포함돼있지만, 이미 B 는 방문했기 때문에 큐에 다시 집어넣지 않는다는 점을 기억해야 한다.

queue.dequeue()   // E
queue.enqueue(H)

큐는 [ F, G, H ] 가 된다. 방문한 적 없는 인접한 노드가 없는 F 를 디큐한다.

queue.dequeue()   // F

큐는 [ G, H ] 가 된다. 방문한 적 없는 인접한 노드가 없는 G 를 디큐한다.

queue.dequeue()   // G

큐는 [ H ] 가 된다. 방문한 적 없는 인접한 노드가 없는 H 를 디큐한다.

queue.dequeue()   // H

큐는 이제 비게 되고, 이는 모든 노드들을 다 탐색했다는 뜻이 된다. 방문한 노드들의 순서는 A , B , C , D , E , F , G , H 이다.

이를 트리로 나타내면 다음과 같다.

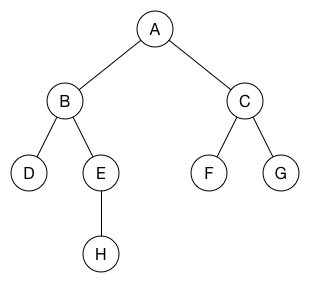
부모 노드는 해당 노드를 “발견한” 노드를 말한다. 트리의 루트는 너비 우선 탐색을 시작한 노드가 된다.

unweighted 그래프이기 때문에 이 트리는 시작 노드부터 모든 다른 노드들까지의 거리가 가장 짧은 것을 의미한다. 그러므로 너비 우선 탐색은 그래프 상의 두 노드 간 최단 거리를 찾을 때 사용하는 방법 중 하나이다.

그래프 상에서 edge(여기선 그냥 노드라고 생각)들이 모두 동일한 무게를 가지고 있을 경우 unweighted 라고 한다. ‘최단 거리’의 맥락에서 봤을 때, 각 레벨의 노드들이 각각 동일한 만큼 떨어져 있다고 생각하면 될 것 같다.

코드

큐를 사용한 간단한 너비 우선 탐색 구현은 다음과 같다.

해당 코드는 너비 우선 탐색의 알고리즘 동작을 보여 주는 것으로, Swift에는 Graph, Node, Queue와 같은 자료형이 정의되어 있지 않다. 실행하고 싶다면, 모든 요소들을 다운받을 수 있는 원문을 참조하자.

func breadthFirstSearch(_ graph: Graph, source: Node) -> [String] {
    var queue = Queue<Node>()
    queue.enqueue(source)

    var nodesExplored = [source.label]
    source.visited = true

    while let node = queue.dequeue() {
        for edge in node.neighbors {
            let neighborNode = edge.neighbor
            if !neighborNode.visited {
                queue.enqueue(neighborNode)
                neighborNode.visited = true
                nodesExplored.append(neighborNode.label)
            }
        }
    }

    return nodesExplored
}

큐에 노드가 있는 동안, 첫번째 노드를 방문하고 그와 동시에 아직 방문하지 않은 인접 노드들을 인큐한다.

코드를 플레이그라운드에서 실행시켜보자.

let graph = Graph()

let nodeA = graph.addNode("a")
let nodeB = graph.addNode("b")
let nodeC = graph.addNode("c")
let nodeD = graph.addNode("d")
let nodeE = graph.addNode("e")
let nodeF = graph.addNode("f")
let nodeG = graph.addNode("g")
let nodeH = graph.addNode("h")

graph.addEdge(nodeA, neighbor: nodeB)
graph.addEdge(nodeA, neighbor: nodeC)
graph.addEdge(nodeB, neighbor: nodeD)
graph.addEdge(nodeB, neighbor: nodeE)
graph.addEdge(nodeC, neighbor: nodeF)
graph.addEdge(nodeC, neighbor: nodeG)
graph.addEdge(nodeE, neighbor: nodeH)
graph.addEdge(nodeE, neighbor: nodeF)
graph.addEdge(nodeF, neighbor: nodeG)

let nodesExplored = breadthFirstSearch(graph, source: nodeA)
print(nodesExplored)

이는 ["a", "b", "c", "d", "e", "f", "g", "h"] 과 같은 결과를 도출하게 된다.

BFS, 뭐에 좋은데?

너비 우선 탐색 알고리즘은 많은 문제를 푸는 데 사용된다. 예를 들어,

• 소스 노드(처음 노드)와 다른 노드들 간의 최단거리를 계산할 때(단, unweighted 그래프에서만)
• unweighted 그래프에서 최소 신장 트리(MST, Minimum Spanning Tree)를 계산할 때

와 같은 경우가 있겠다.

출처

Written by Chris Pilcher and Matthijs Hollemans